numpyやchainerでのベクトル、行列、テンソルの積関連演算まとめ
年末年始にテンソル積と格闘しわけがわからなくなったのでメモ。
numpyのいわゆる積と呼ばれるAPIには、
numpy.multiply, numpy.dot, numpy.vdot, numpy.inner, numpy.cross, numpy.outer, numpy.matmul, numpy.tensordot, numpy.einsumとまあ結構たくさんあります。
特にnumpyについてまとめますが、chainerやtensorflowで同名のAPIが存在する場合、numpyと同じインターフェイスで設計されていますのでほぼ同じ計算をします(はずです)。
コンテンツ
- 要素ごとの積(*,numpy.multiply)
- ベクトルの積(numpy.dot, numpy.vdot, numpy.inner, numpy.cross, numpy.outer)
- 行列積(numpy.matmul)
- テンソル積(numpy.tensordot)
- テンソル積(numpy.einsum)
要素ごとの積(*,numpy.multiply)
A * Bとnumpy.multiply(A, B)は全く同じ意味で、後者はあまり見かけません。
どちらも同じ要素同士をかけます。
という感じです。そのままですね。
同位置にある要素同士の積を実行しますので、異なるサイズ同士では実行できません。
ただし、次元数が異なる2つのndarrayをかけた場合、broadcastが可能な時は、次元数が小さい方のndarrayがbroadcastされて要素ごとの積が実行されます。
例えば0階行列(つまりスカラー)と2x2の2階行列をかけた場合、スカラーを全要素同一の値を持つ2x2の2階行列として扱います。
ベクトルの積(numpy.dot, numpy.vdot, numpy.inner, numpy.cross, numpy.outer)
numpy.dot, numpy.vdot, numpy.innerはベクトル同士のいわゆる内積とかドット積と呼ばれる積を計算します。
dotとvdotは、実数で使っている限りは違いがなく、vdotが使われることはありません。
ベクトルAの要素に複素数が存在する場合、Aの複素共役をとってからドット積を計算するのがvdotです。
電気工学系で虚数単位にiでなくてjを使うのは、iが電流の大きさの変数としてよく使われるからだそうですが、Pythonでjになっているのはiがインデックスによく使われる文字だからでしょうか。わかりません。
numpy.dotと numpy.innerの違いはさらに微妙で、理解するためには後述するテンソル積におけるある軸についての足し上げの知識が必要です。
結論をいうと、A及びBが2次元以上の時、innerは両テンソルの最後の次元同士を足しあげるのに対し、dotはAの最後の次元と、Bの最後から二番目の次元を足し上げます。
しかしそんな細かい規則は覚えてられないので、2次元以上のテンソル積には後述するtensordotかeinsum使ってくれという感はあります。
numpy.crossはいわゆる三次元空間における2つのベクトルについて、定義される、クロス積です。
クロス積は四次元以上のベクトルには定義できません。ValueErrorになります。
ベクトルの代わりに行列が入力された場合、A,Bを最後の階についてのベクトルのリストと解釈され、それぞれのクロス積の結果がスタックされたものが出力になります。
うまく日本語にできないので例を上げます。
numpy.outerは一般化された外積を計算します。外積といわれると、私はどちらかといえば、numpy.crossで計算されるものを私は想像していたのですが、numpy.outerは

なる行列CをベクトルA,Bから計算します。ここでcijは行列Cの(i, j)番目の成分です。
行列積(numpy.matmul)
numpy.matmulはいわゆる二階行列同士の行列積です。
行列積を忘れちゃった人は高校数学を思い出しましょう。
A,Bが二階行列同士の場合は普通に行列積を計算しますが、三階以上のテンソルの場合、A及びBを最後の二階行列に対するリストと解釈して、行列積を計算し、それらの結果をすべてスタックします。
うまい日本語が見つからないので具体例を書き出します。
上記のコードは最後のアサーションをパスします。ここで、
ではA[0,:,:]とB[0,:,:]およびA[1,:,:]とB[1,:,:]の行列積をそれぞれ計算し、その後numpy.stackを使って結果を第0軸に対して積み上げています。
A[0,:,:]、B[0,:,:]、A[1,:,:]、B[1,:,:]はすべて2階行列なので行列積を計算できます。
テンソル積(numpy.tensordot)
任意、特に3以上の次元のテンソルについて積を行う場合、numpy.tensordotやnumpy.einsumを使います。
行列までは要素がたかだか二次元ですので、webページに全部を描き上げることができたのですが、それ以上の階数のテンソルとなるとwebページ上でわかりやすく書き出すことができません。
ですので、各要素に着目し、それを一般化した形ですべての要素を表現します。
例えば(i,j)番目の要素がaij である2階行列Aと、(j,k)番目のとbjkである2階行列Bの行列積Cの(i,k)番目の要素cikは

で表されます。この式を式①とします。
式①の具体的な素性が知りたいときは、変数に数字を入れてみましょう。
例えばAもBも2x2の正方行列である時、Cの(0,1)番目の要素c22はi=0, k=1とすればよく
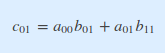
で表されます。
ここで、勘のいい人は、「左辺でjには数字を代入しなくていいの?」と思われたかもしれません。
行列積の場合aにつく最後の添字と、bの最初の添字はダミーと呼ばれ、式①の左辺に現れず右辺で代入しうるすべてのjの値について足しあげられます。
ここで、2階の行列積ではAxBであればAの行およびBの列をかけた結果を足し上げる、という規則をきめていましたが、それ以上の階数のテンソルでの積は足し上げる軸の定め方、すなわちどの添字をダミーとするかを如何様にも決めることができます。
式①のような記法と上記のテンソル積の性質を理解していれば、numpy.tensordotや三階以上のテンソル積も怖くはありません。
numpy.tensordotはa, b, axesの3つの引数を取ります。
ここで、aとbはテンソル積の対象となる2つのテンソルで、axesはどの添字をダミーとするかを指定します。
axesにはintもしくは、((0, 1, 2), (1, 2, 3))のようなintのシーケンスのペアを指定します。シーケンスのペアを指定する場合、2つのシーケンスは同じ長さである必要があります。
int指定した場合、aの最後の(int)番目までの添字と、bの最初の(int)番目までの添字がダミーになります。たとえば、A,Bが三階テンソルの時、
は

となります。
の場合は

となります。添字の順番に注意してください。特に、

でないことに注意してください。
axes=0とした場合は、ダミー指数は存在しません。aおよびb全ての要素の組み合わせについて積を取ったテンソルが出力されます。
axesに((0, 1), (1, 2))のようなintのシーケンスを指定すると、どの添字をダミーとするか直接指定することができます。
すなわち、aについては(0, 1)の軸がダミーとされ、bについては(1, 2)の軸がダミーになります。
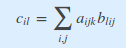
axes=((0, 1), (2, 1))とした場合、各要素は以下のようになります。

テンソル積(numpy.einsum)
最後に残ったnumpy.einsumは、アインシュタインの縮約(Wikipedia)と呼ばれる記法に基づいて添字を用いたテンソルの計算を行います。
詳しくはNumpyのドキュメントを参照してください(←疲れた)
numpy.einsum — NumPy v1.11 Manual
np.einsumはさすがアインシュタインといえるかは知りませんが、本日の記事で紹介したAPI,
すなわち、numpy.multiply, numpy.dot, numpy.vdot, numpy.inner, numpy.cross, numpy.outer, numpy.matmul, numpy.tensordotのすべてを実現出来るだけでなく、numpy.trace、numpy.transposeなど様々なベクトル、行列、テンソルに関する演算を実現できます。
さすがに専用のメソッドがある演算をわざわざeinsumで表現する必要はありませんが、einsumを使わないとごちゃごちゃする演算をeinsum一つでまとめられて、わかりやすくなる場合があり便利です。
また、tensordotなど、今日紹介した多くの演算は一回につき2つのテンソルにしか操作できませんが、einsumは任意個数の演算を扱うことができ、強力です。
感想
tensordotまで書いて、想定以上に記事がボリューミーになり、力尽きました。奥が深い。